Original document by happy sheep/CADUO/喜羊羊第x代. Translated by Steveyboi with Google Translate + DeepL Translate
Contents
ClassWiz QR Function Analysis and Internal Data Storage Principle
Casio launched the ClassWiz series of calculators in 2014, which for the first time implemented a QR code (two-dimensional code) display on a scientific calculator. Scanning the two-dimensional code jumps to Casio’s WES web site, where you can graph function images, histograms, and other charts using exported data, realizing the innovation of a scientific calculator + a handheld device = a graphing calculator.
The QR feature was initially only available on ClassWiz flagship models, and was subsequently extended to non-flagship models, but domestic models have never had access to the feature. As a result, not much has been done to analyze this feature in China, and it has only been covered in some ClassWiz review posts. This document will try to analyze and introduce this feature and the meaning of the encoded content in a more systematic way, and welcome criticisms and corrections if there is insufficient information.
Since the data encoded in QR codes are essentially the computational data of the calculator, this document also deals with the principle of storing data inside the calculator. Fortunately, there is a relatively in-depth study on this topic in the fx-es(ms) bar, so I would like to reintroduce it here as well.

When the exported data is too large, the data will be “split” into multiple QR codes, and the numbers in the lower-right corner indicate the current number and the total number of QR codes. Press [↓], [=], [EXE], or [OK] to display the remaining QR codes in order. You cannot press [↑] to return to the previous QR code, but you can cycle through them.
QR code segmentation is a part of the QR code ISO standard. When creating a segmented QR code sequence, a single QR code encodes the order and total number of QR codes in addition to the data segmented into that segment. Just about no code scanning software we use today is adapted to this split QR code implementation, and will only scan the data of a single QR code, in which case it is necessary to scan the code sequentially and manually merge the data. Casio has proprietary code scanning software that is adapted to this standard, which is also displayed when scanning codes, so that the complete scanning result can be obtained directly.
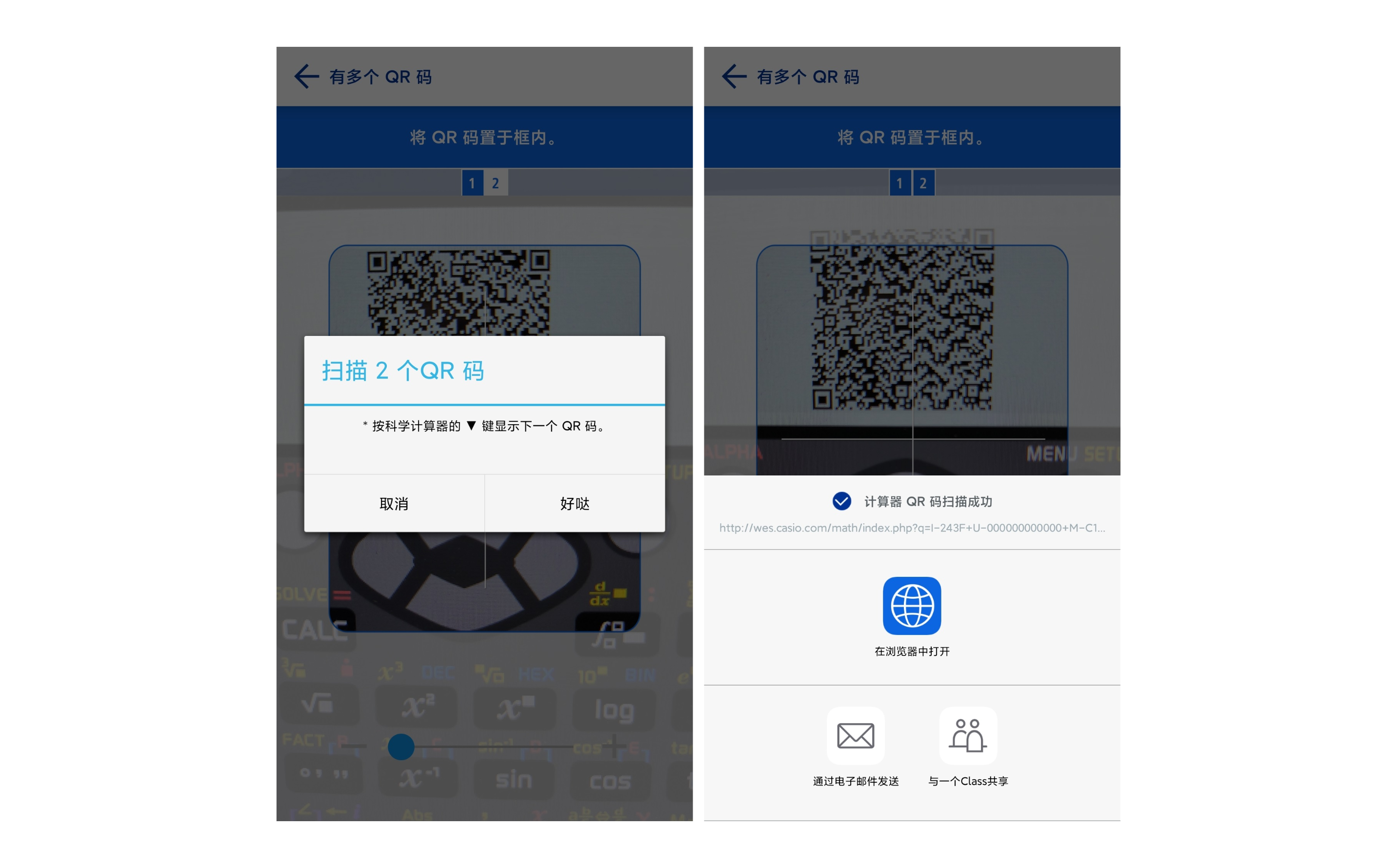
The “version” of the QR code display can be set in Settings, with support for “version 11” and “version 3”, the default is version 11. “Version” is a term used in the QR code specification. In ClassWiz, it is understood that version 3 QR code elements are larger and can be scanned more easily, but the information carried by a single QR code is also smaller. However, the information carried by a single QR code is also smaller. Therefore, the same amount of data would need to be split into more QR codes using version 3. However, the QR code standard supports splitting the data into a maximum of 16 QR codes, so if the amount of data is too large, version 3 QR codes cannot be displayed and “version 3 not supported” will be displayed.

When displaying QR codes, both CW I and CW II support the use of the [←][→] keys to adjust contrast, and the contrast value set here is independent of other screens and is retained when the calculator is reset. CWII also adds an adjustable contrast icon to the lower right corner.
In addition, pressing [5] when a QR code is displayed can cause the mask pattern of the QR code to change, which is never mentioned in the ClassWiz manual. The QR code implementation specification defines 8 different mask patterns, mainly to prevent large white or black blocks from appearing in the QR pattern to improve readability.

QR code content overview
After the introduction of the QR function, let’s look at how QR encodes data. For example, a QR obtained when the fx-JP900CW is in the Mode menu and the cursor is in the “Calculate” mode produces the following after scanning the code:
http://wes.casio.com/ncal/index.php?q=I-031A+U-000000000000+M-X100000000+S-1A93A
As you can see, there is a link with the host name http://wes.casio.com. This is Casio’s “Worldwide Education Service” web site, which until 2022 processed encoded calculation data and returned it to the display on the back end. After 2022, Casio upgraded the service so that accessing this link redirects 302 to the classpad.net website, where richer computing functions can be used.
If it’s the CW I series, the domain name in the link is followed by /math, while for CW II it’s /ncal, which is probably an abbreviation for new calculator. Then the link follows /index.php?q=…… The content after q= is the exported calculation data.
The data is divided into sections, each of which is connected by a + sign; the identifiers of the different sections are indicated by a single macro name, and the identifiers are connected to the stored data by a - sign. Depending on the state of the calculator at the time of the QR, the data in the corresponding section will be reflected. After analyzing the data, the following is a preliminary explanation of the different identifiers:
| Identifier | Guessed name | Explanation |
|---|---|---|
| I | ID | Calculator model and ROM version |
| U | Unique | The serial number displayed during self-test |
| M | Mode | Data such as mode codes, calculation result display methods, etc. stored to indicate how to decode other data |
| S | Setting | Stores data such as calculator setting parameters |
| R | Result | The result area data, generally consists of two parts, each part is 20 in length |
| E | Expression | Generally encoded computational expressions, in Algorithm mode it is the created algorithm |
| T | Tabulation | Spreadsheet data in Spreadsheet mode, or list data in Statistics, Distribution, Math Box, etc. modes |
| C | Chart | Specifically for storing matrix/vector data, also used in Equation mode |
| G | g(x) | Expression of g(x) in Table mode |
| P | Parameter | Table range parameters set to generate function table |
| V | Variable | Occurs when there are variables in the expression of f(x) or g(x), and the value of each variable is stored, except for the x and Ans variables |
| Q | / | Exclusive to CW II models, similar to R, but with 28 degrees of separation per part and used only in normal calculations |
The following is a more detailed introduction to each part of the data
I data
The I data stores the internal model number of the calculator, which is the code shown at self-check, and the ROM version. For example, 243F is shown as CY-243 VerF. As an Easter egg here, the CW I manual includes a screenshot of a QR code example, which is scanned to give the I data as 23B-. Character tables may vary slightly from model to model, for example, European models have a comma at the end of the decimal point, inverse trigonometric functions are shown at the beginning of the Arc, etc., so you will need to know the model number of your model to determine the character table.
| CY self-test number | Model | QR |
|---|---|---|
| 213 | fx-83GT X | 0 |
| 214 | fx-85GT X | 0 |
| 215 | fx-82DE X | 1 |
| 216 | fx-85DE X | 1 |
| 217 | fx-991RS X | 1 |
| 230 | fx-82EX | 0 |
| 231 | fx-85EX | 0 |
| 232 | fx-350EX | 0 |
| 234 | fx-570EX | 1 |
| 235 | fx-991EX | 1 |
| 236 | fx-82CN X | 0 |
| 237 | fx-350CN X | 0 |
| 238 | fx-95CN X | 0 |
| 239 | fx-991CN X | 0 |
| 240 | fx-530AZ | 0 |
| 241 | fx-JP500 | 0 |
| 242 | fx-JP700 | 0 |
| 243 | fx-JP900 | 1 |
| 246 | fx-92 Spéciale Collège | 1 |
| 247 | fx-92B Spéciale Collège | 1 |
| 250 | fx-87DE X | 1 |
| 251 | fx-991DE X | 1 |
| 252 | fx-82SP X | 0 |
| 253 | fx-350SP X | 0 |
| 254 | fx-570SP X | 1 |
| 255 | fx-991SP X | 1 |
| 256 | fx-82AR X | 0 |
| 257 | fx-95AR X | 0 |
| 258 | fx-570AR X | 1 |
| 259 | fx-991AR X | 1 |
| 266 | fx-82SP X II | 0 |
| 267 | fx-350SP X II | 0 |
| 268 | fx-570SP X II | 1 |
| 269 | fx-991SP X II | 1 |
| 270 | fx-82LA X | 0 |
| 271 | fx-350LA X | 0 |
| 272 | fx-570LA X | 1 |
| 273 | fx-991LA X | 1 |
| 291 | fx-82CE X | 0 |
| 292 | fx-85CE X | 0 |
| 293 | fx-350CE X | 1 |
| 294 | fx-991CE X | 1 |
| 295 | fx-92+ Spéciale Collège | 1 |
| 296 | fx-85SP X II | 0 |
| 297 | fx-97SG X | 1 |
| 298 | fx-580VN X | 0 |
| EY self-test number | Model | QR |
|---|---|---|
| 001 | fx-82CW | 1 |
| 002 | fx-85CW | 1 |
| 003 | fx-350CW | 1 |
| 004 | fx-570CW | 1 |
| 005 | fx-991CW | 1 |
| 006 | fx-92 Collège | 1 |
| 007 | fx-92B Secondaire | 1 |
| 008 | fx-82SP CW | 1 |
| 009 | fx-85SP CW | 1 |
| 010 | fx-570SP CW | 1 |
| 011 | fx-991SP CW | 1 |
| 012 | fx-82DE CW | 1 |
| 013 | fx-85DE CW | 1 |
| 014 | fx-87DE CW | 1 |
| 015 | fx-991DE CW | 1 |
| 016 | fx-800DE CW | 1 |
| 021 | fx-82NL | 1 |
| 023 | fx-880BTG | 1 |
| 024 | fx-82CN CW | 0 |
| 025 | fx-95CN CW | 0 |
| 026 | fx-350CN CW | 0 |
| 027 | fx-991CN CW | 0 |
| 028 | fx-999CN CW | 0 |
| 029 | fx-JP500CW | 0 |
| 030 | fx-JP700CW | 0 |
| 031 | fx-JP900CW | 1 |
| 032 | fx-550AZ | 1 |
| 036 | fx-82LA CW | 1 |
| 038 | fx-570LA CW | 1 |
| 039 | fx-991LA CW | 1 |
| 040 | fx-83GT CW | 1 |
| 041 | fx-85GT CW | 1 |
| 044 | fx-8200 AU | 1 |
| 046 | fx-570MY CW | 1 |
| 047 | fx-810DE CW | 1 |
U data
The calculator is written with a 12-digit serial number at the same time as the ROM is flashed at the factory. It is assumed that the serial number stores information about the work produced by the machine, the flow lines, etc., but the more specific coding rules are not clear.
M data
Mode code (1~4)
In the normal calculation interface, digits 1~2 represent the main mode and digits 3~4 are the submode. For example, if Calculate mode has no submode, it will be C100; if it’s the “1-Variable” submode in Statistics mode, it will be 0301.
The following table lists the mode codes and corresponding names with no submode.
| 06 | Matrix |
| 07 | Vector |
| 0D | Spreadsheet |
| 0E | Algorithm |
| 4F | Math Box |
| 88 | Table |
| 89 | Verify |
| C1 | Calculate |
| C4 | Complex |
The following tables give the meanings of each mode code and submode code.
Base-N mode
| 02 | Base-N | 09 | Dec |
| 0F | Hex | ||
| 01 | Bin | ||
| 07 | Oct |
Statistics mode. Among them, the “linear regression” and “quadratic regression” of some models use descending power order instead of ascending power order.
| 03 | Statistics | 01 | Single-Variable Statistic [1-Variable] |
| 02 | Linear Regression [y = a+bx] / [y = ax+b] | ||
| 03 | Quadratic Regression [y = a+bx+cx²] / [y = ax²+bx+c] | ||
| 04 | Logarithmic Regression [y = a+b・ln(x)] | ||
| 05 | exponential Regression [y = a・e^(bx)] | ||
| 06 | ab exponential Regression [y = a・b^x] | ||
| 07 | Power Regression [y = a・x^b] | ||
| 08 | Inverse Regression [y = a+b/x] |
Distribution mode
| 0C | Distribution | 01 | Normal Probability Density [Normal PD] |
| 02 | Normal Cumulative Distribution [Normal CD] | ||
| 03 | Inverse Normal Cumulative Distribution [Inverse Normal] | ||
| 04 | Binomial Probability [Binomial PD] | ||
| 05 | Binomial Cumulative Distribution [Binomial CD] | ||
| 06 | Poisson Probability [Poisson PD] | ||
| 07 | Poisson Cumulative Distribution [Poisson CD] |
Equation mode, of which submode 08 is “Solver”, which is new to CW II.
| 45 | Equation | 01 | Simultaneous Equation | 2 Unknowns |
| 02 | 3 Unknowns | |||
| 03 | 4 Unknowns | |||
| 04 | Polynomial Equation | ax²+bx+c | ||
| 05 | ax³+bx²+cx+d | |||
| 06 | ax⁴+bx³+cx²+dx+e | |||
| 08 | Solver | |||
Ratio mode
| 4A | Ratio | 01 | A:B=X:D |
| 02 | A:B=C:X |
Inequality mode. Among them, the submode code is used to refer to the degree of the polynomial equation, and the sign of the inequality also needs to be determined using 7~8 digits in the M data. For example, M-4B04DD0100 means ax²+bx+c<0
| 4B | Inequality | 04 | 00 | ax²+bx+c>0 |
| 01 | ax²+bx+c<0 | |||
| 02 | ax²+bx+c≥0 | |||
| 03 | ax²+bx+c≤0 | |||
| 05 | 00 | ax³+bx²+cx+d>0 | ||
| 01 | ax³+bx²+cx+d<0 | |||
| 02 | ax³+bx²+cx+d≥0 | |||
| 03 | ax³+bx²+cx+d≤0 | |||
| 06 | 00 | ax⁴+bx³+cx²+dx+e>0 | ||
| 01 | ax⁴+bx³+cx²+dx+e<0 | |||
| 02 | ax⁴+bx³+cx²+dx+e≥0 | |||
| 03 | ax⁴+bx³+cx²+dx+e≤0 |
Result area template (5~6)
Bits 5~6 of the M data are used to indicate the template style displayed in the result area. For example, if the result of calculating Rec(r,θ) has two parts x=a, y=b, 11 is used to refer to it.
| 11 | Rec(r,θ) | x=a,y=b |
| 12 | Pol(x,y) | r=a,θ=b |
| 13 | Solve for ?? | ??=a, L-R=b |
| 14 | ÷R | a,R=b |
| 15 | →Simp | F=b,a |
Among them, 13 is used in the solution interface of SOLVE. The target variable for solution needs to be referred to by digits 9~10 of the M data, which is the hexadecimal code corresponding to the character of the solution variable. For example, if the result is x=a, L-R=b, and it is solved for x, these two digits are 48 (47 in CW II).
For other values, the default is to treat the algebraic form of the complex number a+bi. Even if it is temporarily converted to polar coordinate form r∠θ (use →r∠θ in CW I or use the format menu conversion in CW II), it will not be exported and indicated in the M data of QR. If the default display is set to polar coordinate format, you need to view the S data.
Numerical display format (7~8)
The 7th digit is used to indicate the display format of the result area value, and the 8th digit indicates the format in which it is stored in the variable. For example, if 7~8 is AD, the result needs to be displayed as a decimal, but it can be converted into a standard result display.
| 1 | Degrees minutes seconds format |
| 2 | Press [ENG] 4 times |
| 3 | Press [ENG] thrice |
| 4 | Press [ENG] twice |
| 5 | Press [ENG] once |
| 6 | Press [SHIFT] [ENG] once |
| 7 | Press [SHIFT] [ENG] twice |
| 8 | Press [SHIFT] [ENG] thrice |
| 9 | Press [SHIFT] [ENG] 4 times |
| A | Decimal |
| B | Improper fraction |
| C | Mixed fraction |
| D | Standard |
| E | Recurring decimal |
| F | Prime factorization |
Among them, for the display of engineering notation, after pressing [ENG] for the first time, the decimal point will try to move to the right until the exponent of ×10 is a multiple of 3. If it is already there, it will not move. Continue to press [ENG] to continue moving right, up to 4 times. [SHIFT][ENG] is the same, but it just moves the decimal point to the left. CW II introduced the function of moving the decimal point with the [←][→] keys, and the principle is similar.
Non-calculation screen
If the QR is generated in the error interface, mode menu, or setting menu, the first two digits will be the corresponding error or menu code. At this time, accessing the link will jump to the corresponding manual page.
| X1 | Calculate |
| X2 | Base-N |
| X3 | Statistics |
| X4 | Complex |
| X5 | Equation |
| X6 | Matrix |
| X7 | Vector |
| X8 | Table |
| X9 | Verify |
| XA | Ratio |
| XB | Inequality |
| XC | Distribution |
| XD | Spreadsheet |
| XE | Algorithm |
| XF | Math Box |
| Y1 | AC Break |
| Y2 | Syntax ERROR |
| Y3 | Math ERROR |
| Y4 | Range ERROR |
| Y5 | Cannot Simplify |
| Y6 | Circular ERROR |
| Y7 | Stack ERROR |
| Y8 | Argument ERROR |
| Y9 | Dimension ERROR |
| YA | Cannot Solve |
| YB | Time Out |
| YC | Variable ERROR |
| YE | Memory ERROR |
| YG | No Operator |
| YH | Not Defined |
| YZ | Nesting ERROR (ERREUR branch in French) |
| Z0 | Setup |
| Z1 | Setup (2nd level) |
S data
The length of S data is generally 28 characters, and it stores the calculator’s setting data, such as angle units, etc.
The following table shows the setting names corresponding to characters in different positions, and the setting items corresponding to different parameter values.
| Digit(s) | Setting name | Parameter value | Setting items |
|---|---|---|---|
| 1 | Number Format(Main) | 0 | Norm1 |
| 4 | Norm2 | ||
| 8 | FixX | ||
| 9 | SciX | ||
| 2 | Number Format(Sub) | 0~9 | X in FixX/SciX |
| 3 | Decimal Mark | 0 | Comma |
| 1 | Dot | ||
| 4 | Angle Unit | 4 | Degree |
| 5 | Radian | ||
| 6 | Gradian | ||
| 5 | Input | 0 | LineI |
| 1 | MathI | ||
| 6 | Fraction Result | 0 | d/c |
| 1 | ab/c | ||
| 7 | Complex Result | 0 | a+bi |
| 1 | r∠θ | ||
| 8 | Statistics Frequency | 0 | Off |
| 1 | On | ||
| 9 | Recurring Decimal | 0 | Off |
| 1 | On | ||
| 10 | Simplify | 0 | Auto |
| 1 | Manual | ||
| 11 | Output | 0 | MathO(LineO) |
| 1 | DecimalO | ||
| 12 | Auto Power Off | 0 | 10 Min. |
| 1 | 60 Min. | ||
| 13 | Table Type | 0 | f(x) |
| 1 | f(x),g(x) | ||
| 2 | g(x) | ||
| 14 | Engineer Symbol | 0 | Off |
| 1 | On | ||
| 15 | Digit Seperator | 0 | Off |
| 1 | On | ||
| 16 | Multi-Line Font | A | Small Font |
| E | Normal Font | ||
| 17 | Equation Complex Root | 0 | Off |
| 1 | On | ||
| 18 | Language | / | Vary on Models |
| 19 | Spreadsheet: Auto Calc | 0 | Off |
| 1 | On | ||
| 20 | Spreadsheet: Show Cell | 0 | Formula |
| 1 | Value | ||
| 21 | QR Code Version | B | Version 11 |
| 3 | Version 3 | ||
| 22 | Algorithm: Background | 0 | Axes |
| 1 | Axes/Grid | ||
| 2 | Axes/xy | ||
| 3 | None | ||
| 23 | Algorithm: Unit Setting | 0 | pixels |
| 1 | units | ||
| 24 | Unknown | ||
| 25~28 | Checksum | ||
Among them, the input/output settings are jointly determined by the parameter values of digits 5 and 11. The last four digits are suspected to be calculated through some algorithm, similar to a check code. On some CW I models released earlier, this is used to verify authenticity.
Internal numerical storage principle
The calculator internally uses a method similar to BCD code (Binary-Coded Decimal) to store values. From ES to CW I series, 10 bytes (i.e. 20 digits) are used to store values. CW II uses 14 bytes (28 digits) for storage due to improved accuracy, but there is no fundamental change in the storage methods of the two.
Some data exported from QR, such as R data, also export the values stored in the calculator as hexadecimal, but the format has been changed.
Let’s first take the 10-byte and 20-digit storage method as an example to see how it is stored inside the calculator, and then talk about the similarities and differences between it and the exported data.
When the value is 0, all 20 digits are 0.
If it is not 0, taking \(1.23456789112345\times 10^{67}\) as an example, the value will be stored in the calculator in the following form:
01234567891123456701
Area ①: The first digit is the type flag, which marks the storage type format of the value;
Area ②: The 2nd digit to 5th digit from the right is the significant number storage area. You can see that it occupies 15 digits, which corresponds to 15 digits of significant digits;
Area ③ and area ④: The fourth and third digits from the right and the first and second digits from the right are the sign and exponent digits. For different storage formats, the meanings of the two areas will be slightly different.
The following is an introduction to each storage format.
Floating point format
The floating point format (area ①) flag is 0. When storing a value, the calculator intercepts 15 significant digits and writes it in scientific notation with only 1 digit in the integer part, and stores it in area ②. If the exponent in scientific notation is >0, area ③ stores the exponent directly, if the value itself is >0, area ④ takes 01, otherwise it takes 06. If the exponent in scientific notation is <0, the inverse of the exponent, i.e., 100-|exponent| is used in area ③. In this case, if the value itself is >0, area ④ takes 00, otherwise it takes 05.
| Area ③ | Area ④ | |
|---|---|---|
| Exponent>0, value>0 | Exponent | 01 |
| Exponent>0, value<0 | Exponent | 06 |
| Exponent<0, value>0 | 100-exponent | 00 |
| Exponent<0, value<0 | 100-exponent | 05 |
Here are some examples to facilitate understanding
- Writing 123456789 as \(1.23456789000000\times 10^{08}\), both the number and the exponent part are >0, so it will be stored as
01234567890000000801 - By intercepting the first 15 significant digits of \(0.0000987654321123456789\) and write it as \(9.87654321123456\times ^{-05}\), the number is >0, the exponent part is <0, and 100-5=95, then
09876543211234569500 - \(−201420202022\times ^{−23}\), will be written as \(−2.01420202022000\times ^{−12}\), the number is <0, the exponent part is also <0, and 100-12=88, then
02014202020220008805
Fraction format
The fraction format flag is 2. When storing a fraction, if the absolute value of the fraction is <1, the fraction line is represented by A and stored in area ② in the form of numerator A fraction, with 0 padding after less than 15 digits. If the absolute value of the fraction is >1, it needs to be converted into a mixed fraction and then stored in the form of integer A numerator A fraction. The 15th bit is also supplemented with 0. This is essentially the same as the linear input representation of the fraction. Area ③ is the “length” of the fraction, as explained below with an example. Area ④ is the symbol of the fraction, if it is a positive number, it will be 01, and if it is a negative number, it will be 06.
- \(\frac{2}{3}\) is expressed as
22A30000000000000301 - \(-\frac{2}{300}\) is expressed as
22A30000000000000506
In the above two examples, underlines are used to mark the length of the fraction. You can see that area ② of both is 2A3000000000000, but due to the difference in area ③, the values expressed are different. - \(\frac{56789}{1234}>1\), converted to a mixed fraction \(46\frac{25}{1234}\), then
246A25A1234000001001
Under normal circumstances, the length of a fraction cannot exceed 10. If the operation exceeds 10, it will be converted into a floating point number for storage and cannot be converted back. This is also why some fractions that do not seem to exceed the calculation range are still expressed as decimals. It is probably because the length of the number is expressed as an improper fraction and is not greater than 10, but the length is expressed as a mixed fraction. The degree is over 10. If the value of the corresponding variable in an emulator is modified through an exception or using a memory editor, it can still be displayed.
Degrees minutes seconds format
The degrees minutes seconds format flag is 4.
At this time, it uses the same storage method as floating point numbers, except that the calculator converts it into degrees, minutes and seconds format by default when displaying.
Radical format
The radical format flag is 8. The calculator can display the addition of up to two different radical expressions, which can be called radical expression 1 and radical expression 2. Each radical expression can have up to 3 digits. The coefficient of the radical expression is a fraction. The numerator can have up to 2 digits. The two fractions can be different, and the two fractions will be displayed when displayed.
For example, there is radical 1: \(\sqrt{aaa}\times\frac{bb}{cc}\) and radical 2: \(\sqrt{ddd}\times\frac{ee}{ff}\), they will be stored in area ② as
aaa bb cc 0 ddd ee ff
It occupies exactly 15 bits, and the 0 in the middle can be understood as a separator.
At this time, area ③ is used to indicate the positive and negative sign of radical formula 2, and area ④ is used to indicate the positive and negative sign of radical formula 1. Similarly, the positive number is 01, and the negative number is 06.
- \(-\frac{12\sqrt{345}}{67} + \frac{78\sqrt{777}}{89}\) will be stored as
83451267077778890106 - \(\sqrt{3}\) can be written as \(\sqrt{000}\times\frac{00}{01}+\sqrt{003}\times\frac{01}{01}\), then
80000001000301010001 - \(2-\frac{\sqrt{7}}{2}\) can be written as \(\sqrt{001}\times\frac{02}{01}-\sqrt{007}\times\frac{01}{02}\), then
80010201000701020601
For example 1 above, when the calculator displays the result, it will be divided into \(\frac{5226\sqrt{777}-1068\sqrt{345}}{5963}\) for display, but if this formula is entered into the input area for calculation, it will exceed the limit of the radical format, and the result will be converted and stored as floating point format.
ERROR value
The error value flag is F. Normally no ERROR value is stored in the variable, to create an ERROR value, there is the TABLE method in ES PLUS, and in CW I, you can type the following equation, and then press [CALC][=][=], M will light up, [AC]. Check the value of M is empty. Recall M directly to get a math error. Looking at the memory, the memory area where M is located begins with F3, and in the analysis of the M data described above, Y3 corresponds to a math error.
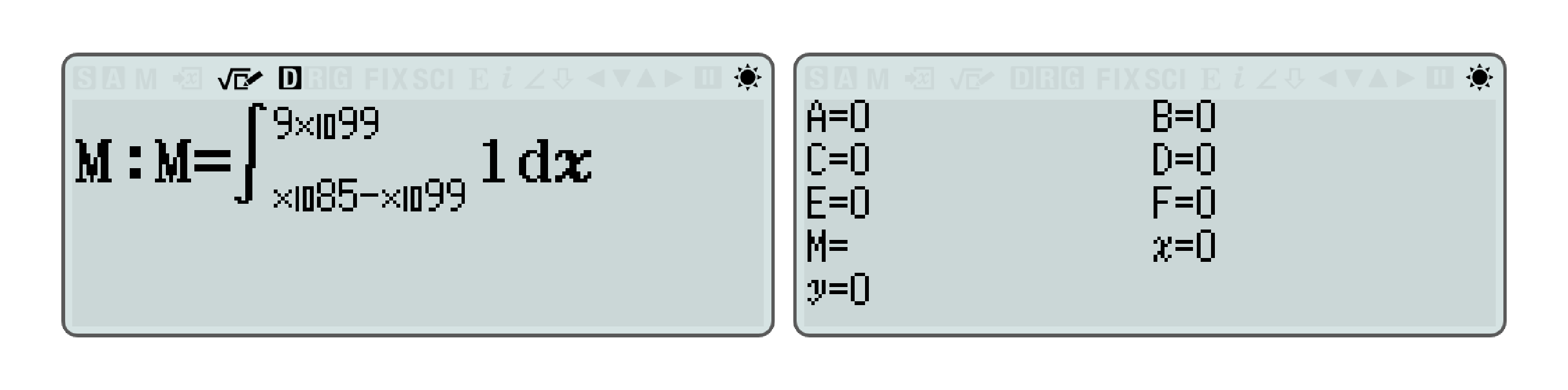
If you enter \(=\div\) in Table mode, a cell with syntax error will be created, and after exporting with QR, the value stored in that cell (how to check it will be explained later) starts with F2, which happens to be the syntax error corresponding to Y2 in the M data.
In other words, although all values starting with F are ERROR values, they are also reserved.
Others
In fact, the internal storage will also have data with flag digit 6, which is equivalent to a pointer to a matrix or vector. Since QR directly derives the values stored in the matrix, it will not be described here.
Numerical representation of CW II
CW II increases the precision to 23 digits and uses 14 bytes and 28 digits to store floating point numbers, but the representation method does not fundamentally change. The last 4 digits are also used to store area ③ and area ④. The floating point number format needs to occupy the middle 23-bit area ②, and the remaining numerical formats are padded with 0s.
- \(9.0000000000000000075528\) is represented as
0900000000000000000755280001 - \(\frac{570}{991}\) as
0570A99100000000000000000701
The length of the fraction still cannot exceed 10 - \(-\frac{12\sqrt{345}}{67}+\frac{78\sqrt{777}}{89}\) as
8345126707777889000000000106
8 zeroes are padded in area ②
R data
Now that the storage principle of internal values has been introduced, let’s take a look at how the QR function exports these values.
Different from the internal storage method, the R data exported by QR will swap the positions of area ③ and area ④.
Calculate, Complex modes
When R data is exported on the screen of ordinary calculation results, it needs to be divided into two parts, each of which has 20 digits, which corresponds to the 20 digits of the internal storage method.
If the calculation result is relatively “simple”, such as the result of a numerical operation, the second part of the R data is all 0, and only the first part (the first 20 digits) is useful, and can be parsed according to the storage method described above (the positions of area ③ and area ④ need to be swapped).
If the calculation result is relatively “complicated” and the calculator uses two parts for display, such as the Pol and Rec coordinate operations, the ÷R remainder operation, the result of an imaginary number in Complex mode, etc., it is necessary to parse the two parts of the R data and determine the method for displaying the two values according to the corresponding parameters in the M data.
- After exporting the calculation result \(1.23456789112345\times 10^{67}\), the R data will be
0123456789112345016700000000000000000000
Please note that the positions of area ③ and area ④ have been reversed. - The result of calculating \(\textrm{Pol(1, −1)}\) is \(r = \sqrt{2},\theta = −45\), which is derived as
8000000100020101000104500000000000000601 - \(\frac{5}{7} - \sqrt{2} + \sqrt{3}i + 2i\), at this time the first part is the real part and the last part is the imaginary part
8001050700020101010680010201000301010101
In addition to ordinary calculations, when calculations involving equations, inequalities, matrices, vectors, and other calculations contain multiple results, there will be a storage flag for this data at the beginning of the R data, followed by numerical value parts, each of which is also 20 bits, and the results corresponding to the numerical values of each part will be decided based on the M data and the storage flag at the beginning of the R data.
Equation mode
For example, when solving a certain linear equation, we get \(x = -\frac{9}{7}, y = \frac{15}{7}\). At this time, the R data is (newlines have been added to improve readability)
EQ0
21A2A700000000000605
22A1A700000000000105
EQ indicates the result in Equation mode, and EQ0 indicates that the equation has a solution. If it is EQ1, it is “Infinite Solution”; EQ2 is “No Solution”; EQ4 is “No Real Roots”; if a model is able to find the minimum and maximum values of its corresponding function when solving a cubic equation, it will start with EQ5, or EQ0 if it is not supported.
Matrix, Vector
If in matrix mode, the calculation result is a matrix \(\begin{bmatrix} 0 & 1.41421356237309 & 1.23456789112345\times 10^{67} \\ −4.56987123\times 10^{-6} & \frac{1}{7} & -\frac{8}{9} \\ \end{bmatrix}\)
The R data will be
MT23
00000000000000000000
01414213562373090100
01234567891123450167
04569871230000000594
21A70000000000000103
28A90000000000000603
The M at the beginning means Matrix; MT means MatAns. 2 and 3 indicate that the matrix is 2×3 in size. The following values are the values from left to right and top to bottom of the matrix.
Similarly, if it is a vector result, it starts with VT, that is, VctAns, but for two- and three-dimensional vectors, VT02 and VT03 will be used instead of VT12 and VT13.
Inequality
In Inequality mode, there are similar expressions:
| Prefix | Meaning |
|---|---|
| IN01 | All Real Numbers |
| IN02 | No Solution |
| IN03 | \(x=a\) |
| IN04 | \(x\neq a\) |
| IN05 | \(x<a\) |
| IN06 | \(x\leq a\) |
| IN07 | \(a<x\) |
| IN08 | \(a\leq x\) |
| IN09 | \(a<x<b\) |
| IN0A | \(a\leq x\leq b\) |
| IN0B | \(x<a, b<x\) |
| IN0C | \(x\leq a, b\leq x\) |
| IN0D | \(x=a, b\leq x\) |
| IN0E | \(x\neq a\mathrm{\ and\ }x<b\) |
| IN0F | \(x\leq a, x=b\) |
| IN10 | \(a<x\mathrm{\ and\ }x\neq b\) |
| IN11 | \(a<x<b,c<x\) |
| IN12 | \(a\leq x\leq b,c\leq x\) |
| IN13 | \(x<a,b<x<c\) |
| IN14 | \(x\leq a,b\leq x\leq c\) |
| IN15 | \(x\neq a\mathrm{\ and\ }x\neq b\) |
| IN16 | \(x=a,x=b\) |
| IN17 | \(x\neq a\mathrm{\ and\ }x<b,c<x\) |
| IN18 | \(x=a,b\leq x\leq c\) |
| IN19 | \(a<x<c\mathrm{\ and\ }x\neq b\) |
| IN1A | \(x\leq a,x=b,c\leq x\) |
| IN1B | \(x<a,b<x\mathrm{\ and\ }x\neq c\) |
| IN1C | \(a\leq x\leq b,x=c\) |
| IN1D | \(a<x<b,c<x<d\) |
| IN1E | \(x<a,b<x<c,d<x\) |
| IN1F | \(a\leq x\leq b, c\leq x\leq d\) |
| IN20 | \(x\leq a,b\leq x\leq c,d\leq x\) |
At this time, the R data starts with INxx, and is followed by each value in the order of corresponding \(abcd\).
Verify mode
The R data in verification mode has only 20 bits, representing a value, “True” is 1, “False” is 0.
Q data
Q data is newly added to CW II, and its format is similar to R data. It consists of two parts, each part is 28 bits, and the positions of area ③ and area ④ should also be reversed.
It is also necessary to determine the display format of the read value based on the M data. For example, in Complex mode, \(\frac{2}{3} - \sqrt{7}i + 9i\) is expressed as
22A30000000000000000000001038001090100070101000000000106
Q data will only be exported in normal calculations. Multiple results in equation, matrix and other modes are still exported in R data. (Casio lazy dog programmer confirmed)
C data
The storage format of C data is similar to that of R data. Each part is also 20 bits, and the positions of area ③ and area ④ are reversed.
When in Matrix or Vector mode, the QR code generated by any operation will carry C data, which contains defined matrix or vector information. Similar to R data, if it starts with MA23, it means MatA, and the size is 2×3; VA03 means VctA, a three-dimensional vector.
When in Equation and Inequality mode, the C data represents the input equation coefficient. At this time, there is no flag at the beginning, and the type of equation or inequality is determined based on the M data to determine the number of coefficients.
When in Distribution or Math Box mode, the C number carries the input parameter value. The type and number are determined by the corresponding sub-mode, and there is also no mark at the beginning.
P data
A QR code generated in Table mode will carry this data, indicating the start value, end value and step of the generated number table. The data consists of three parts, each part has 9 digits. The representation method is similar to the 20-digit number of R data, but it is regarded as a floating point number, so the identifier at the beginning is removed. There are only 6 significant digits. The positions of area ③ and area ④ are also reversed, and area ④ only retains the second half of the digits (0, 1, 5 or 6).
For example, the P data with a start value of \(9.8765\times ^{-43}\), an end value of \(12345\), and a step length of \(4567.89\) will be expressed as
987650057
123450104
456789103
V data
In function table mode, if the defined f(x) or g(x) expression contains variables, the generated QR will carry the data.
The format is similar to P data, the length is also 9 digits, and the effective digits are only 6 digits. The data stored in CW I are the values of ABCDEFyM in order. If it is CW II, the last one is the value of the z variable.
T data
Spreadsheet mode
Different from the previous Matrix and other modes where all values are exported in order, the QR code exported from the spreadsheet only carries the values written into the cells with data. This is achieved by encoding the writing status of the cells.
The T data of the data table starts with SP, followed by 60-bit cell identifier data to identify which cell has a value. The identifier data is compressed by converting binary to hexadecimal, and the order is column first, then row.
For example, if there is data in rows 1, 3, and 4 of column A, from top to bottom, if the value is written, it will be represented by 1, and if it is not written, it will be represented by 0, at this time, you will get \(1011_{(2)}\), that is, \(B_{(16)} )\), so the first 3 characters of T data are obtained as SPB. By analogy, the numerical writing status of the remaining cells is obtained, and converted into hexadecimal representation.
Since each column has 45 rows of data, the calculator uses 12 characters to fully represent a column (whether the cell in row 45 writes data or not will make the last character either \(0000_{(2)} = 0_{(16)}\), or \(1000_{(2)} = 8_{(16)}\)). There are 5 columns of cells, so 60 characters are used as cell identifiers. What follows these 60 characters is the value of the cell where the data has been written.
That is to say, divide the 60 characters after SP into 12 parts, convert them into binary, add 0 to the front if there are less than 48 digits, and then remove the last 3 digits, the resulting 45 numbers will represent the data writing status of 45 cells in each column in turn.
Formulas cannot be exported in Spreadsheet mode, the exported data only has numerical values, the format is similar to P data, and there are only 6 significant digits. If the formula generates an ERROR, the exported data of the corresponding cell starts with Fx, corresponding to the respective ERROR type.
Statistics mode
In statistics mode, the data in the statistics list is exported. The numerical format is also similar to P data. There are only 6 significant digits and should occupy 9 characters.
But at this time, the T data uses compressed storage. The 9 characters are divided into 3 parts, regarded as decimal numbers, and then converted into base 32, so that its number of digits is reduced to 2 digits, the occupancy is reduced from the original 9 characters to 6.
For example, the format of \(1.23456\times 10^{78}\) written as P data is 123456178, and
\[123_{(10)} = 3R_{(32)}\\ 456_{(10)} = E8_{(32)}\\ 178_{(10)} = 5I_{(32)}\]then the value will be expressed as 3RE85I
In turn, the encoded T data is divided into every 2 characters, regarded as base 32, converted into a decimal number, and then spliced in sequence to obtain the original numerical storage format.
The order of exporting data is row first, then column, and the number of columns (x columns, y columns and frequency) needs to be determined based on the M data.
Distribution pattern
When using the distribution calculation type of list calculation, the results of the current calculation can be exported, and the data is in T data. There are also only 6 valid digits, and every 9 characters represent one piece of data, without compression.
Expression character principles
When inputting an expression, each character has a corresponding storage method inside the calculator, and their mapping relationship is the well-known “first-level character table”. The ClassWiz series began to introduce double-byte characters. Generally, the high-order FA, FB, FD, FE, and the low-order values 01-EF are meaningful characters. Therefore each character takes 1 or 2 bytes to store.
If it is a linear input format, you only need to search and replace each hexadecimal character in the character table to convert it into readable characters. But in the case of mathematical input, special processing must be done to the natural writing template.
Currently, ClassWiz has 14 natural writing symbol templates. Among them, recurring decimals have been adjusted according to the habits of different regions, and there are 3 expression methods.
| Natural writing template | Source code |
|---|---|
| \(XX\frac{YY}{ZZ}\) | 18 1F 1D 1A XX 1B 1A YY 1B 1A ZZ 1B 1E |
| \(\dot{X}\dot{X}\ \overline{XX}\ (XX)\) | 2F 1A XX 1B |
| \(\sum_{x=YY}^{ZZ}(XX)\) | 50 1A XX 1C YY 1C ZZ 1B |
| \(\int_{x=YY}^{ZZ}(XX)\) | 51 1A XX 1C YY 1C ZZ 1B |
| \(\frac{\mathrm{d}}{\mathrm{d} x}(XX)\biggr\rvert_{x=YY}\) | 52 1A XX 1C YY 1B |
| \(\prod_{x=YY}^{ZZ}(XX)\) | 53 1A XX 1C YY 1C ZZ 1B |
| \(\rvert XX \rvert\) | 68 1A XX 1B |
| \(e^{XX}\) | 72 1A XX 1B |
| \(10^{XX}\) | 73 1A XX 1B |
| \(\sqrt{XX}\) | 74 1A XX 1B |
| \(\log_{XX}(YY)\) | 7D 1A XX 1C YY 1B |
| \(\frac{XX}{YY}\) | C8 1D 1A XX 1B 1A YY 1B 1E |
| \(\Box ^{XX}\) | \(\Box\) C9 1A XX 1B |
| \(\sqrt[XX]{YY}\) | CA 1D 1A XX 1B 1A YY 1B 1E |
XX, YY, and ZZ in the template symbols in the above table correspond to the corresponding positions of the source code in sequence and can be nested. In the source code, 1A, 1B, 1D, and 1E can be seen as pairs of brackets (); 1C is similar to a comma, or ),(; 1F is special and is only used with 18, a mixed fraction.
Algorithm command storage principle
In algorithm mode, characters with the high byte F9 are used to store commands.
TI-Planet has compiled a mapping of the characters and corresponding commands used by fx-92+ Spéciale Collège: (added English text for fx-92B Secondaire)
F901 : end of line
F902 : end of program
F903 : nop / empty line
F905 ... 00 : Avancer de ... (Move)
F906 ... 00 : Tourner de ... (Turn)
F907 ... 00 : S'orienter à ... (Direction)
F908 ... 00 ... 00 : Aller à x=... ; y=... (Go to x,y)
F909 : Stylo écrit (Pen Down)
F90A : Stylo relevé (Pen Up)
F90B ... 00 ... 00 : ... → ... (mettre var à/Set Variable to)
F90C ... 00 : ? → ... (Demander valeur/Ask and assign)
F90D3100 : "Oui" (Yes)
F90D3200 : "Non" (No)
F90D3300 : "Nombre?" (Number?)
F90D3400 : "Résultat:" (Result :)
F90E ... 00 : Afficher résult ... (Show Result)
F90F3100 : Style Flèche (Arrow Style)
F90F3200 : Style Croix (Cross Style)
F910 : Attendre (Wait)
F911 ... 00 : Répéter ... (Repeat)
F912 : ⤴ (end of Répéter/Repeat)
F913 ... 00 : Répéter jusqu'à ... (Repeat Until)
F914 : ⤴ (end of Répéter jusqu'à/Repeat Until)
F915 ... 00 : Si ... Alors [... Fin] (If ... Then [... End])
F916 : Fin (End) (end of Si/Alors / If/Then)
F917 ... 00 : Si ... Alors [... Sinon ... Fin] (If ... Then [... Else ... End])
F918 : Sinon (Else)
F919 : Fin (End) (end of Si/Alors/Sinon / If/Then/Else)
The editable area in the command stores the expression as it is entered, and uses 00 as the terminator for data input in a single command.
The command data is not stored in the input area (the first buffer), but in a place relatively behind the memory area.
E data, G data
In modes other than algorithm, the exported E data is the hexadecimal digits of the characters in the current input area and is exported as is without any change.
In algorithm mode, the source code of the command is exported to the E data as is.
G data is the expression of g(x) derived in Table mode.
References
- 【991+boring tutorial】Set Ans=2/0, and the principle can be retained after booting. https://tieba.baidu.com/p/1899977141
- 【Technology】Research on internal numerical storage. https://tieba.baidu.com/p/2793407170
- 【ClassWiz Joint Test】Comparison of Casio flagship models 991CNX/JP900/991DEX/991SPX. https://tieba.baidu.com/p/3894270548
- Classwiz/fx-92+SC tokens encoding. https://tiplanet.org/forum/viewtopic.php?f=27&t=21662